|
Ever since I first shared my Inquiry Cube designs on this website back in 2015, it has been fun to see how they have been used by many different teachers all over the world. (1, 2, 3) Each of the levels that I created were designed so that students had many different patterns to interpret and determine what is on the missing side. In each of those levels, there was one target answer that students were trying to uncover. While it achieved my goal of building grit and providing students with an opportunity to find success in a challenging task on the first day of the year, this lesson design also left behind a really wonderful feature of the original lesson plan that inspired this idea.
Uncertainty and the Nature of Science
In science, we are often looking for patterns to make predictions about the world around us. Sometimes, the reality that we are predicting can be measured to confirm or disprove our theories but many times, all we are able to do is to add evidence and reasoning to support our ideas knowing that we may never know for certain. The original lesson plan that first introduced me to the inquiry cube concept included a feature that the lesson ended without a reveal or confirmation that their predictions were correct. I still remember that unsettled feeling I had in my teacher prep grad school course when I realized that we were never going to find out the answer. I was reminded of this last summer at the Perimeter Institute's EinsteinPlus Workshop when their version of the task highlighted more than one possible interpretation, so not only did we not receive an answer from the instructors but our answers didn't even necessarily match the other groups around us.
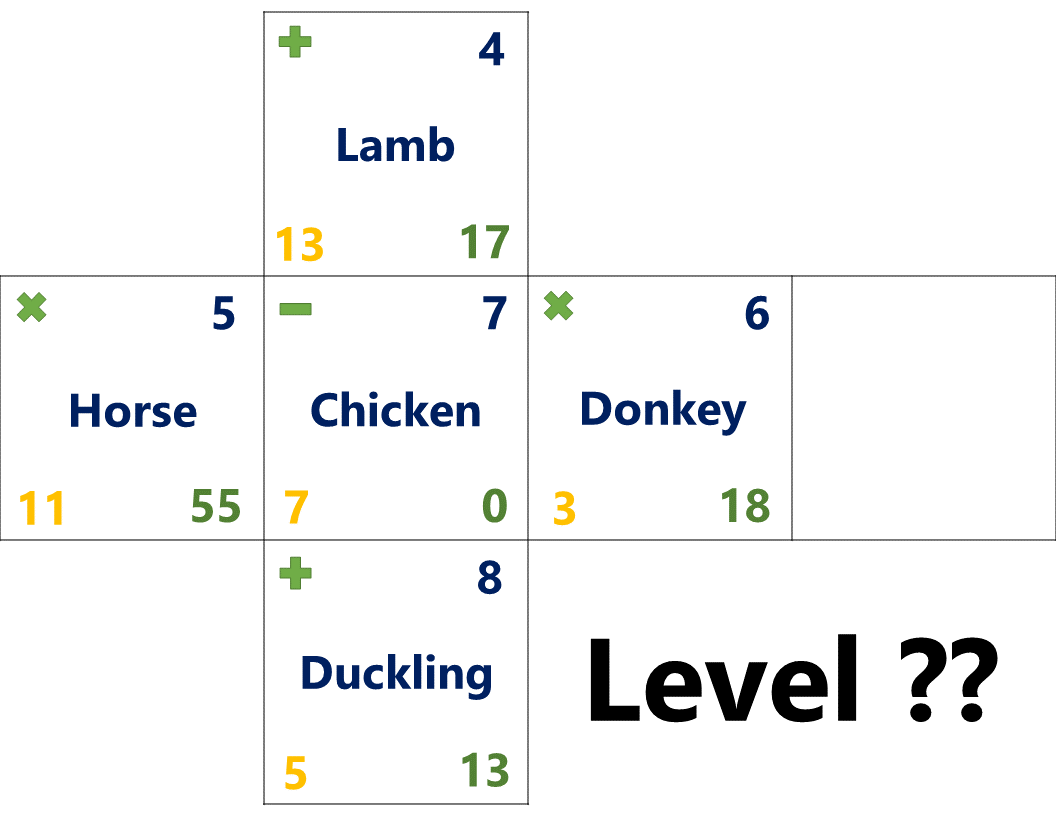
Level ?? | A Cube with Many Answers
The Patterns
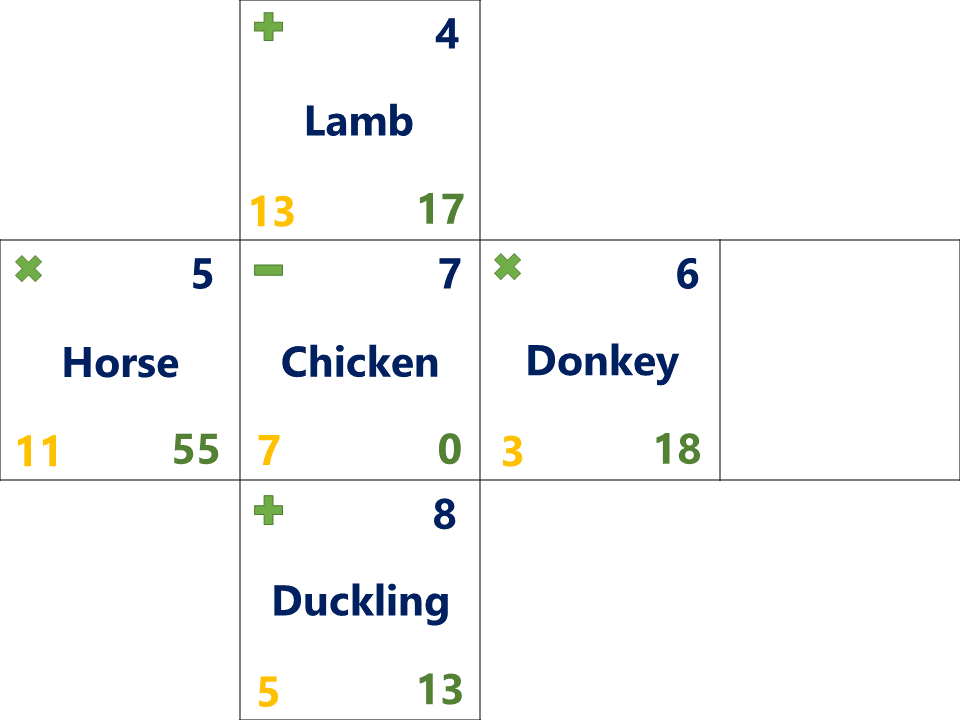
As mentioned earlier, the intention with this cube was to have as many "correct" answers as possible. In the sections below, I will try and outline some of the interpretations that have been designed into the cube. As the goal here was ambiguity, there are likely other ways that students can defend patterns that they see so this list is not intended to be exhaustive. If you haven't tried it for yourself yet, I would recommend looking it over in the image above first before continuing so you can have the experience of a student before seeing any "answers". ;)
Top Left
This is probably the most straight forward of the different patterns. Each side contains the same mathematical operation as the side opposite from it. With this logic, one could expect that the missing side should have a subtraction symbol in the top left corner.
Top Right
The known values for this corner are 4, 5, 6, 7, and 8. From these, it is reasonable to assume that it is a consecutive numerical sequence but it doesn't necessarily have a guaranteed starting value. Because of this, the missing side could contain a 3 if it is a sequence from 3-8 or a 9 if it is a sequence from 4-9.
Bottom Left
The known values for this corner are 3, 5, 7, 11, and 13. This set of numbers has three possible 6th values but it is a little less obvious.
Bottom Right
The solution to this value is found by studying mathematical formula created by the other corners on that side of the cube. (for example on the "Donkey" side, 3 x 6 = 18) Because of this and the multiple interpretations for the other patterns, there are several possible answers. To make it a little more interesting, the cube is designed so that it ambiguous what order the operation should take place. For all of the other known examples, they are either multiplication/addition and therefore operate under the commutative property (i.e. 3 x 6 = 18 and 6 x 3 = 18), or they are subtraction that results in zero (7-7 = 0) so there aren't any examples that inform whether it should be “(bottom left)[top left](top right)=“ or “(top right)[top left](bottom left)=“. This means that a subtraction problem on the missing side could reasonably result in a positive or negative number. Based on the scenarios already outlined above, there could be nearly a dozen evidence-based interpretations before adding the final pattern.
Middle
For the final pattern, there is a word in the center of the cube that contains the number of letters to match the top right corner. Depending on the rule that is decided on by the students, this could be made more specific if desired to help limit responses. For instance all of the examples shown are farm animals so it could be assumed that the missing side must contain a farm animal as well. Even with a more specific rule in mind, there are multiple examples that could fit for a given number of letters. If the top left number is 3, students could logically conclude that the missing animal is "cat", "pig", "hen", "cow" or any other farm animal with 3-letters. Because of this, students are even less likely to arrive at the same answer as their peers and may seek other patterns to help argue for their solution. Lessons on Nature of Science
With this cube design, there are several takeaways and conversations that can come up related to the nature of science
Scientists can't always test to see if a theory is correct
As mentioned before, this design works best if there is no "correct answer" reveal at the end. In real life, it is rare when a theory can be fully confirmed. Instead, theories are tested and strengthened by adding evidence and reasoning to support them.
Sometimes a pattern looks different depending on perspective
A great way to go about this activity is to have students compare their work with others and take note of similarities and differences. It is useful to focus these conversations on the process and patterns that led to their answers. As shown above, the patterns included in this puzzle are designed to have multiple interpretations but there is a no reason that the rules I used have to be the end-all either. Take the bottom left pattern for instance -- personally, my first inclination is that a 9 fits the pattern by filling the "hole" in the odd number pattern 3-5-7-9-11-13. This assumes that the numbers must make a sequence. If the determined rule is that it just has to be an odd number, it could just as reasonably be 15 or 63 or 1057. It would be a really valuable extension for students to try and "rethink" their answers when they are done to see what other interpretations might exist.
Sometimes nature limits our options
In this cube, many of the patterns interact with each other and these interactions can help limit the possible responses. For example, with the interpretation that the top left corner is a straight numerical sequence, we can expect that the middle animal has either 3 or 9 letters. I don't know about you, but I can think of far more 3-letter animals than 9-letter animals so while either is possible, the 3 seems more likely. That said, failing to see something doesn't necessitate that the thing is really not there. Sometimes a theory is determined by the most likely scenario and it comes down to our ability to dream up the scenario in the first place. Files
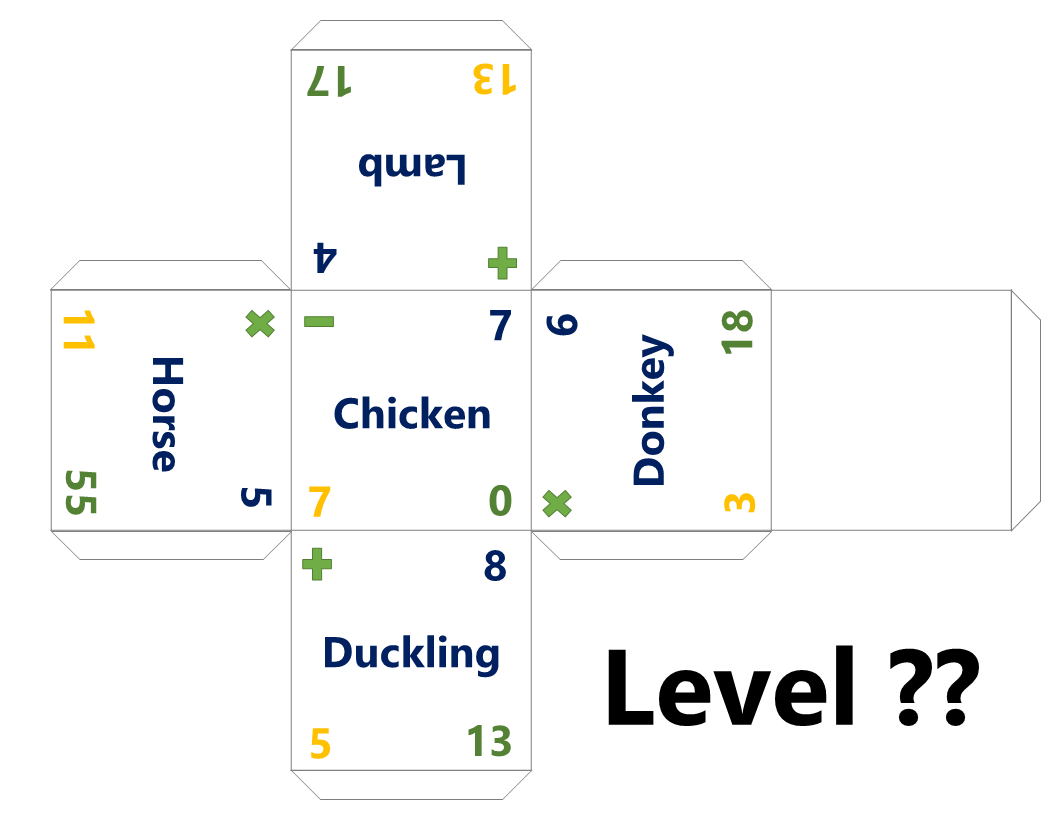
Click below to download the files for this cube design. The files contain the design, a printable version with flaps to fold and glue, and an answer key outlining some of the potential patterns.
Virtual Inquiry Cube
In an effort to make this activity accessible for online learners, I have also created a virtual cube that can be manipulated by clicking and dragging. Nothing beats a physical, hands-on experience , but this virtual cube at least makes the activity possible without students needing to spatially interpret an unfolded cube design.
Acknowledgements
This updated design would have never happened had it not been for the Perimeter Institute and EinsteinPlus workshop. If you haven't seen it yet, be sure to check out their version of this inquiry cube task in the Nature of Science resource.
I especially want to thank Laura Pankratz (@laura_pankratz) for pushing my thinking on the purpose of this task and serving as a thought partner and guinea pig through the first iterations of this idea. :)
Comments
|
Joe CossetteFather, Physics Teacher, Knowles Fellow, Friend, Techie, and Musician Blog Posts |
||||||||||||||||||||||||||||||||




 RSS Feed
RSS Feed

